博客作者的优势：尝试一丝不解地思考和清晰的逻辑，以促进读者。

⛳️Motto：一百英里的人中有一半是九十。

本文的目录如下：

目录

1个概述

在磁场和电场中移动的带电颗粒的轨迹可以用洛伦兹的力定律描述。洛伦兹的力量定律描述了电场和磁场中带电颗粒的联合力，其表达是：

F = Q（E + V×B）

其中，f是由带电颗粒暴露的联合力，Q是颗粒的电荷量，E是电场的强度，V是颗粒的速度，而B是磁场的强度。 “×”是指跨多头。

根据洛伦兹的力量定律，在电场和磁场的综合作用下，带电颗粒的速度和加速度将变化，从而导致轨迹偏转。在三维空间中，粒子的轨迹取决于初始条件，包括粒子的初始速度，其初始位置以及电场和磁场的特性。

在恒定的磁场中，带电的颗粒将遵循螺旋轨道，称为洛伦兹轨道。这是因为磁场在粒子上施加垂直于速度方向的力，从而导致颗粒连续弯曲中心值，从而形成螺旋轨道。

在存在电场的情况下，电场将迫使带电的颗粒，从而导致颗粒加速或减速。因此，带电颗粒的轨迹将不再是一个简单的螺旋形状，而是会因电场力的影响而变化。

应该注意的是，粒子的质量，电荷，速度，磁场和电场特征等因素将影响轨迹的形状和特征。因此，根据系统的参数和初始条件，需要通过数值模拟或分析方法来解决特定的轨迹方程。

总而言之，当带电颗粒在磁场和电场中移动时的轨迹是一个复杂的问题，具体取决于颗粒的初始条件以及磁场和电场的性质。通过洛伦兹的力量定律，可以描述其合并力，但是需要根据特定情况进一步分析和计算特定的轨迹方程。

有限的差异方法用于求解带电颗粒在均匀磁场或均匀电场或跨磁场的运动方程式以及源自洛伦兹力量定律的电场。 MScript的图形输出总结了模拟中使用的参数，

XY平面和3D轨道和位移，速度和加速度图中的轨迹。

2个运行结果

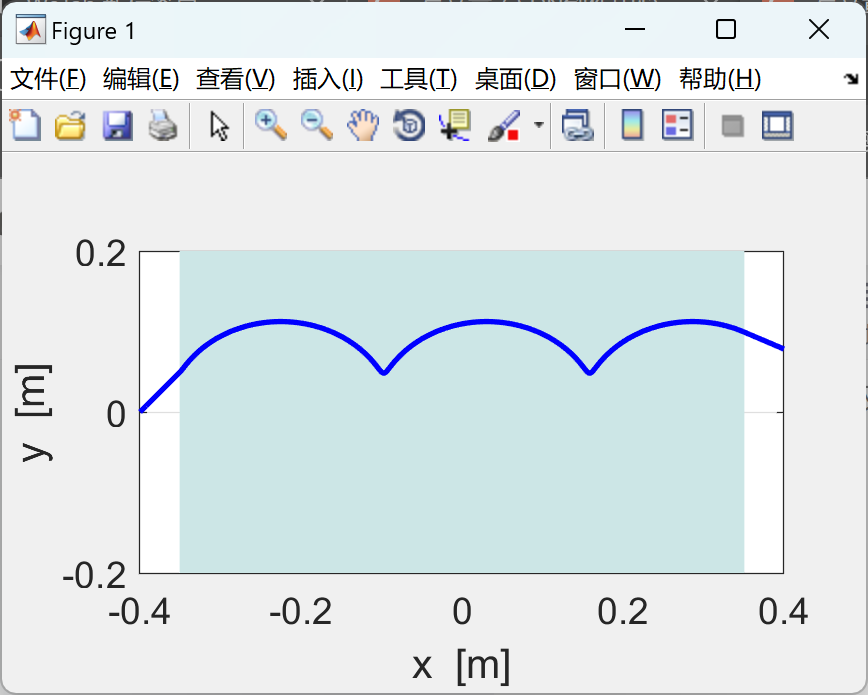
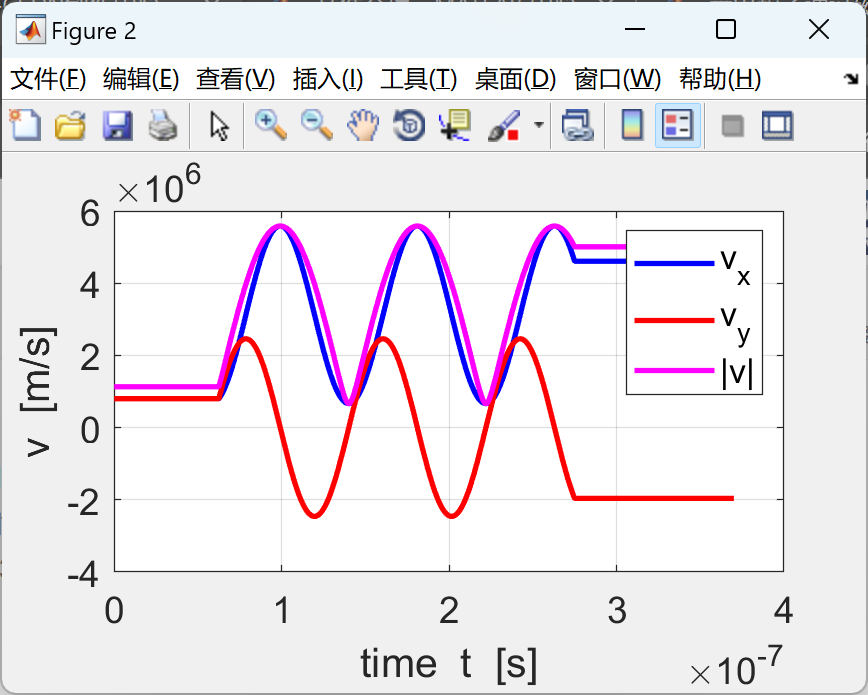
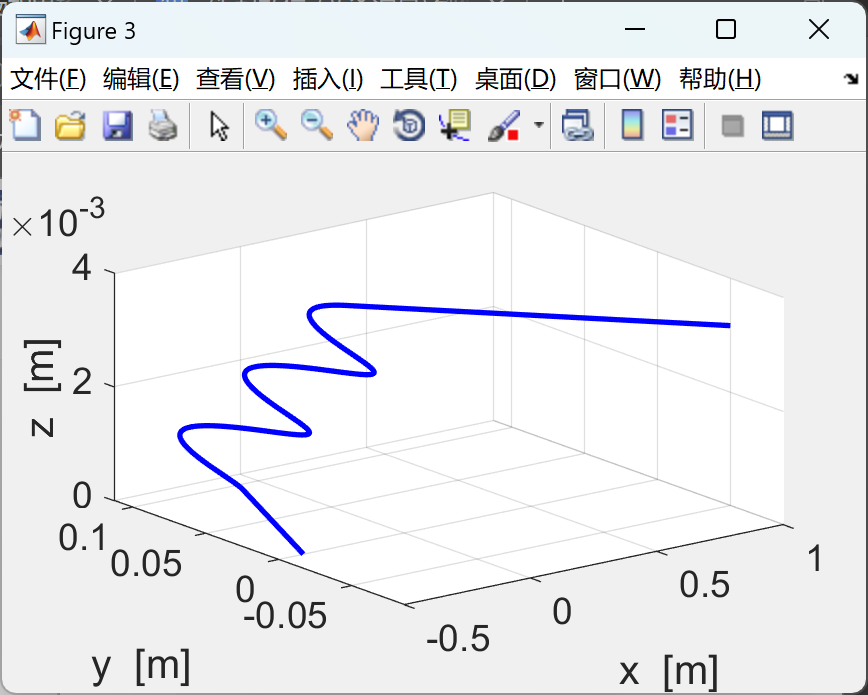
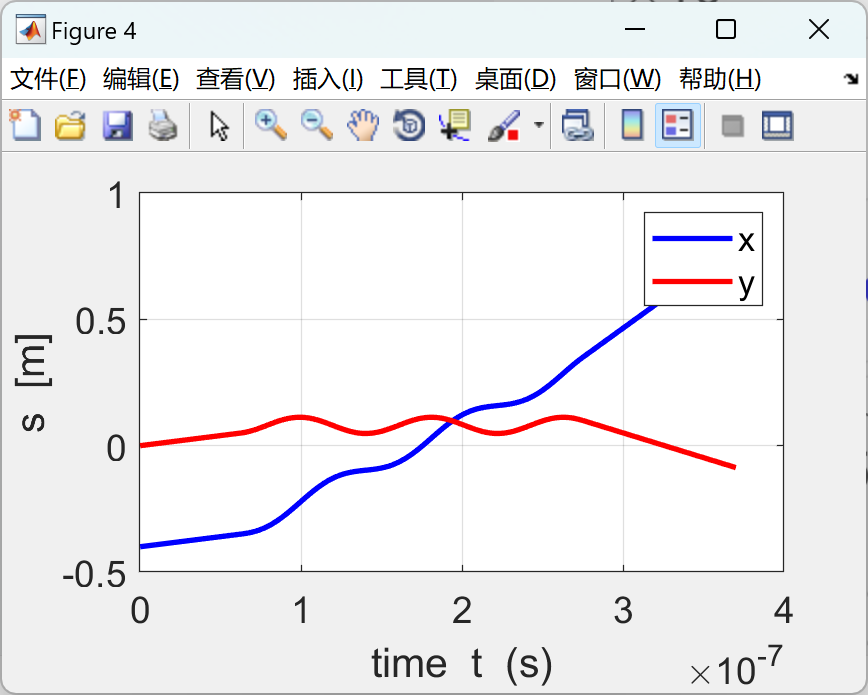
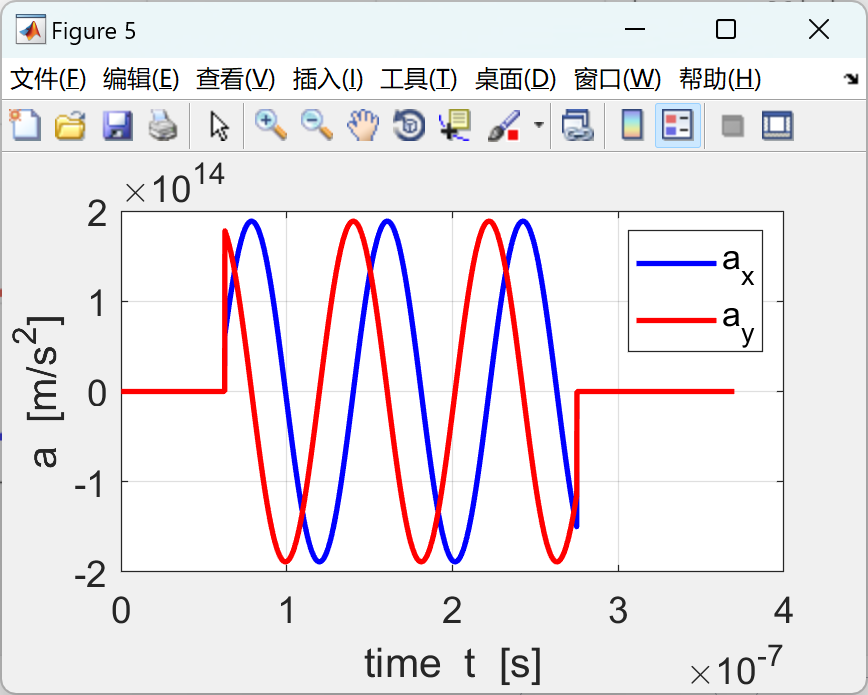
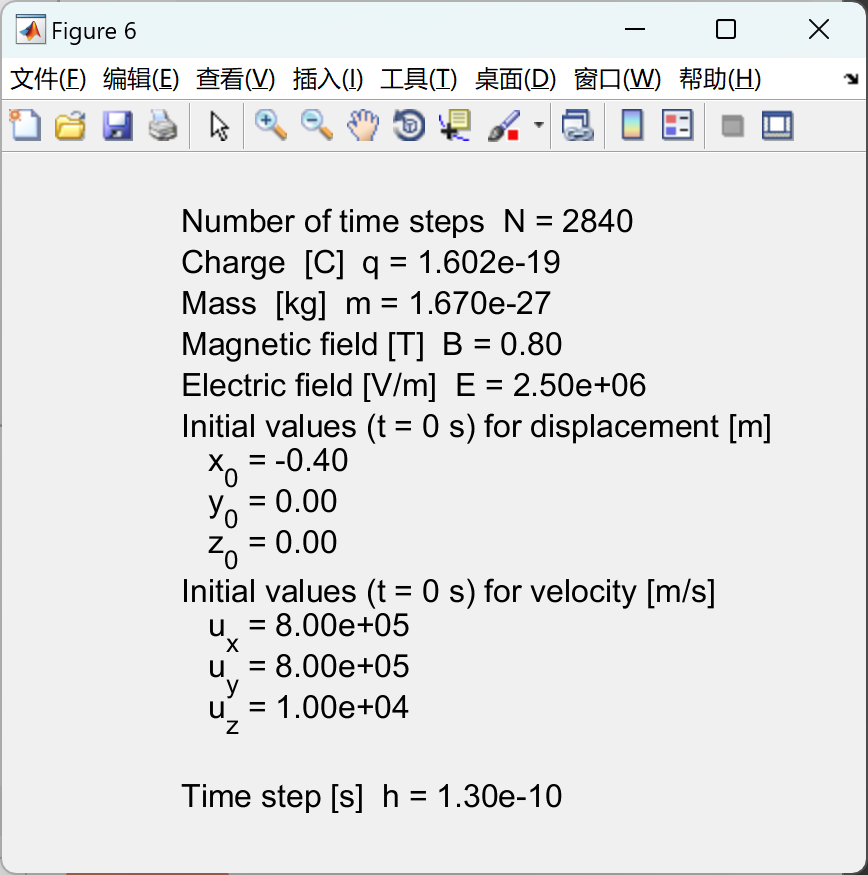
代码的一部分：

图（5）％------------------------------------------------------------------ -----------------------

set（gcf，“单位”，“归一化”，“位置”，[0.36,0.1,0.3,0.3]）;

xp = t; yp = ax;

情节（xp，yp，'b'，'lineWidth'，2）

坚持，稍等

xp = t; yp = ay;

情节（XP，YP，'r'，'lineWidth'，2）

Xlabel（'Time T [S]'）;

Ylabel（'a [m/s^2]'）;

传奇（'a_x'，'a_y'）;

网格

set（gca，'fontsize'，14）;

图（6）％-------------------------------------------------------------------------------------- -----------------------

set（gcf，“单位”，“归一化”，“位置”，[0.67,0.1,0.3,0.4]）;

XP = 0; yp = 0;

情节（xp，yp，'b'，'lineWidth'，2）

轴（[0 100 0 100]）;

FS = 12;

px1 = 10; py1 = 98; dpx = 5; dpy = 7; px2 = 50;

元素数量n

tx1 ='时间步长n =';

tx2 = num2str（n，'％4.0f \ n'）;

tx3 ='';

tx = [TX1 TX2 TX3];

h_text = text（px1，py1，tx）; set（h_text，'fontsize'，fs）;

百分比收费q

py1 = py1 -dpy;

tx1 ='电荷[c] q =';

tx2 = num2str（q，'％2.3e \ n'）;

tx3 ='';

tx = [TX1 TX2 TX3];

h_text = text（px1，py1，tx）; set（h_text，'fontsize'，fs）;

百分比电荷m

py1 = py1 -dpy;

tx1 ='质量[kg] m =';

tx2 = num2str（m，'％2.3e \ n'）;

tx3 ='';

tx = [TX1 TX2 TX3];

h_text = text（px1，py1，tx）; set（h_text，'fontsize'，fs）;

％磁场B

py1 = py1 -dpy;

tx1 ='磁场[t] b =';

tx2 = num2str（b，'％2.2f \ n'）;

tx3 ='';

tx = [TX1 TX2 TX3];

h_text = text（px1，py1，tx）; set（h_text，'fontsize'，fs）;

％电场e

py1 = py1 -dpy;

tx1 ='电场[v/m] e =';

tx2 = num2str（e，'％2.2e \ n'）;

tx3 ='';

tx = [TX1 TX2 TX3];

h_text = text（px1，py1，tx）; set（h_text，'fontsize'，fs）;

轴熄灭

初始位置％xyz

py1 = py1-1*dpy;

tx1 ='初始值（t = 0 s）用于位移[m]';

tx2 ='';

tx3 ='';

tx = [TX1 TX2 TX3];

h_text = text（px1，py1，tx）; set（h_text，'fontsize'，fs）;

py1 = py1-1*dpy;

tx1 ='x_0 =';

tx2 = num2str（x（1），'％2.2f \ n'）;

tx3 ='';

tx = [TX1 TX2 TX3];

h_text = text（px1，py1，tx）; set（h_text，'fontsize'，fs）;

py1 = py1 -dpy;

3个参考